This is going to be another boring post. It’s specifically regarding how the app shuffles cards and randomness in general but its also going to get into things like statistics and heuristics.
The short story is that new cards show up in order during their first study session. This is because I like to edit my cards from the Study View and I’m usually working from a list. If you don’t want new cards to show up in order there is a setting you can enable to randomize them. For cards that are not new, I use arc4random_uniform([array count]) to choose random numbers and a Fisher-Yates shuffle to actually shuffle the cards. Even though these procedures may seem to be the best and/or most standard ways of getting random numbers and shuffling a set, you might still notice patterns and/or the resulting shuffles might not seem random to you. How can that be?
Computers are not really capable of choosing things at random. Generally speaking, when one asks a computer to generate a random number it must go through some process to create that number. It might use the current time or some other internally-known condition (voltage, temperature, etc.) as a basis for generating the number. If we could recreate the precise condition or conditions that existed in a system when it generated a random number, we could cause that system to generate the same random number over and over again. That’s not truly random. The same thing is true of the universe. If you precisely reproduce the conditions of the universe (and I mean the precise position, velocity, and spin of every fundamental particle in existence), you will always get the same outcome (quantum fluctuations not withstanding). Even though you may think you have free will, you wouldn’t be able to change your mind if everything were precisely the same. Given the same conditions, you must always choose Pepsi instead of Coke. Given the same conditions.
I personally prefer Coke, by the way. But there must be some conditions that would cause me to choose Pepsi. I can’t really imagine what those conditions might be but if they existed, I must choose Pepsi. And if we recreated those conditions precisely through many trials, I would choose Pepsi every time. Get it? I would not be able to change my mind.
But, can that really be true? Certainly, you can change your mind and random things do happen all the time, right? Well, now we’re getting into a philosophical debate. What does random mean? Does it mean something that seems random to people and not something that is actually random in the mathematical sense? If we’re only concerned about things that seem random to people then, yes, randomness does exists. If we’re talking about mathematical randomness…actually, I’m not sure.
I think truly random things may not exist (again, ignoring the quantum world) but what we can do is try to reach a state of being as random as possible and call that state mathematical randomness. It’s just like circles. While we can mathematically describe a circle, in fact there seem to be none. There seems to be nothing in existence that is actually round. There are very round things. Things that are so round that they are almost truly round. Things like the sun – the roundest thing we know of. But we are capable of measuring the fact that it is not round. What we mean when we call something round is that it is round enough to be practically round. What I mean when I say random is just random enough to be practically random.
So, let us ignore the possibility that randomness may not even truly be possible. Let’s just establish a model with two phrases: seems to be random and mathematically random. Seems to be random will simply mean that it’s difficult for the average person to notice a pattern and mathematically random will mean that it’s actually approaching a smooth distribution curve.
When I implement a random function, such as a function that should shuffle or choose virtual flashcards at random, do I want mathematical randomness or do I want something that seems random to people? Well, wait a second. Shouldn’t that be the same thing? If it’s as random, or pseudo-random as it were, as it’s possible for a computer to be, won’t that also seem random to people?
Almost certainly not. Humans, generally speaking, are horrible at statistics. We do not have a natural affinity for it. What we do have a natural affinity for is patterns. We seek them out. Visual patterns such as faces. We see them where they do not exist. We see faces in burnt toast and in clouds and in mountain shadows on Mars. There are no faces there but we see them all the same. We also seek out numerical patterns. No, I’m not talking about those math problems from your tests in junior high school. I’m referring to numerical patterns that we may not even realize are related to numbers and/or statistics such as patterns in the occurrence of events.
There is a very good reason for this pattern seeking behavior. It’s so you don’t have to waste time and energy actually using your brain to think about things all the time. Your brain is an amazing piece of biological machinery. And like many other amazing pieces of machinery, it’s an energy hog. Despite what you may have heard or read elsewhere, unless you had a developmental abnormality or some sort of inadvertent head trauma, you use 100% of it at almost all times and it consumes as much as 30% of the energy your digestive system extracts from the food you eat. Actually, I’m not sure about that energy number as I’ve seen estimates ranging from 20-25% and heard seemingly well-informed people mention numbers as high as 30%. Anyway, it is the single most draining organ that you posses. That’s good because it makes you really smart. But it’s also kinda bad because it consumes a lot of energy. Because of this, it has various built-in efficiency systems that it makes use of in order to keep the amount of energy it requires to a minimum.
One of these systems or perhaps series of systems manifests itself as something known as heuristics. This goes directly back to patterns in the occurrence of events. It’s quite simple to see A and then B and know that A caused B. Especially if we see this sequence occur over and over again. A and B may in fact be completely unrelated or due to some unobserved and unknown third condition but heuristics might cause us to simply link A and B. Likewise, if I see A, B, and then C and notice some similarity or relationship between the three (for example, they’re the first three letters of the Roman alphabet in order) then I might have a tendency to think that something fishy is going on if I had been told that I would be shown random letters.
But is it really fishy? Can I deduce fishiness after seeing only three trials? What’s the likelihood or mathematical probability that you would get A, B, and then C randomly? Certainly, it’s not 0 but I don’t know what the actual probability is because I’m not good at statistics. I could work it out but that’s not the point. The point is, I can’t immediately see the answer or even easily find it after a bit of thought. I would have to really think about it. Perhaps even get out a pencil and sheet of paper to figure it out.
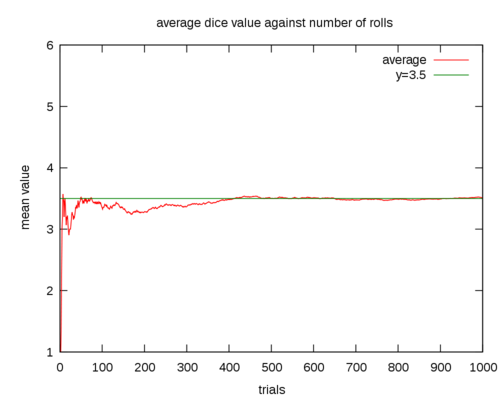
I don’t think that you can really figure out anything statistically speaking after only three trials. In fact, you would probably need to see quite a large number of trials in order to get a good spread. The more the better. So, if you notice that a few of your cards show up in order or near each other or in reverse order or whatever pattern you happen to notice, what does that mean? What if the same pattern occurs twice in a row? Despite the fact that you may feel like something strange is going on, it’s probably quite normal. Even unlikely things have some probability associated with them. The fact that they are not impossible means that they must eventually occur. If you really want to show that something fishy is going on, do a thousand or so trials, work out the probability spread that you observed and compare it to what you would consider random. You’ll probably notice that there’s only a few tenths of a percentage difference between what you would expect and what you actually observed. Which would mean…nothing fishy.
I could implement checks to make sure that the seemingly fishy things don’t occur. I could make sure cards don’t get shuffled back into their original positions. I could ensure that cards that were created within a short interval of each other or cards that feature the same kanji don’t get shuffled into positions near each other. I could ensure that the same patterns that occurred in a previous shuffle don’t occur in subsequent shuffles. However, doing these things would actually make the shuffles less random. It would seem more random to the casual observer but these arbitrary tricks would actually destroy the overall distribution. So, even though seemingly fishy things might (or almost certainly will) occur, I think I’m going to just leave the current implementation as is. It may not seem very random but I actually think that means it’s approaching the standard of randomness I would prefer to see.
Happy studies!
What the user wants…the user will get: Study Due Variance